Suatu kuantitas vektor dapat direpresentasikan secara grafis
dengan garis, yang ditarik sedemikian rupa sehingga :
a. Panjang garisnya menandakan maknitudo kuantitas tersebut, sesuai skalanya.
a. Panjang garisnya menandakan maknitudo kuantitas tersebut, sesuai skalanya.
b. Arah
garis (ditunjukkan dengan anak panah) menandakan arah bekerjanya kuantitas
vektor tersebut.
Kuantitas vektor
AB disebut sebagai AB atau
a.
- Dua vektor yang sama
- Jika dua vektor
a dan b sama maka keduanya memiliki magnitudo dan arah yang sama.
-
Jika dua vektor a dan b memiliki
magnitudo yang sama dan arah yang berlawanan maka a = -b.
- Jenis – jenis vektor
- Vektor posisi
AB terjadi apabila titik A
tetap, suatu vektor yang titik awalnya 0.
Jika A(x,y,z) maka OA = a (x,y,z) dan
|a| =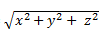
|a| =
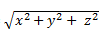
-
Vektor garis ialah sedemikian rupa
sehingga vektor itu dapat digeser disepanjang garis .
- Vektor satuan adalah suatu vektor
panjangnya satu.
Vektor arah sumbu x, sumbu y, dan sumbu z
berturut- turut adalah:
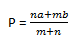
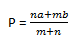
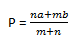
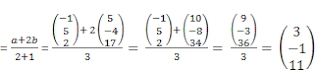
i = (1 0 0) ; j = (0 1 0) ; k = (0 0 1)
- Penambahan vektor
- Jumlah dari dua vektor AB dan BC , didefinisikan
sebagai vektor tunggal atau vektor ekuivalen atau vektor resultan AC.
AB + BC = AC atau a
+ b = c
- Jumlah dari beberapa vektor a + b + c + d + .....
-
Vektor yang tergambar seperti rantai
AB + BC + CD + DE = AE
Atau
a + b + c + d = AE
- Jumlah dari beberapa vektor (resultan) yang membentuk diagaram vektor berupa bangun tertutup sebesar 0 (nol)
a + b + c + d = 0
- Besar atau panjang vektor
b. Jika
A (a1, a2, a3) dan B (b1, b2, b3) maka
|AB|= 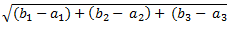
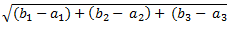
- Perbandingan
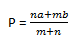
a,p,dan b adalah vektor – vektor posisi dari titik A, B dan P.
- Contoh soal
1. Jika a = (3 2 5), b = (-4 6 7) , c = (2 -1 3)
Vektor
2a + b – 3c = ....
Jawab :
2a + b – 3a = 2(3 2 5) + (-4 6 7) - 3(2 -1 3)
= (6 4 10) + (-4 6 7) + (-6 3 -9)
= (-4 13 8)
2. Diketahui titik A(-1,5,2) dan B(5,-4,17),
jika titik P membagi AB sehingga AP:PB= 2:1, maka vektor posisi titik P
adalah....
Jawab :
Pakai rumus perbandingan :
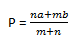
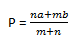
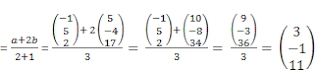
Cara lain :
AP : PB = 2 : 1
P -a = 2 ( b-p)
P -a = 2b – 2p
p + 2p = a + 2b
3p = a + 2b
p = a + 2b => sama dengan cara pertama
3








